파이썬, class, Exception, 시간복잡도 공간복잡도, Big-O Notation

class 

 

파이썬은 그 자체로 객체라고 할 수 있을만큼 대표적인 객체 지향 프로그래밍(OOP) 언어이며,  class는 객체 지향 프로그래밍에서 사용되는 중요한 개념이다.

 

class는 데이터 타입을 만든다는 거고, class에는 '속성'과 '행동'이 있어야 한다.

 

속성은 class 안에서 정의된 변수 → 즉, 객체가 가지고 있는 '데이터'

행동은 class 안에서 정의된 함수 → 즉, '메서드'

 

 

[ 메서드의 종류 ]

 

1. 인스턴스 메서드

• 우리가 주로 사용하는 메서드로, 인스턴스 번수를 사용하거나, 인스턴스 변수에 값을 설정한다.
• 클래스 내부에 정의되는 기본 메서드다.
• 호출 시, 첫번째 인자로 인스턴스 자기자신(self))가 자동으로 전달된다.
• 메서드를 호출한 인스턴스를 의미하는 self 매개변수를 통해 인스턴스를 조작한다.
• 참고로, 클래스의 변수를 변경할 때는 항상 클래스.클래스변수 형식으로 변경 한다. 

class Person:

    def __init__(self, name):
        self.name = name

 

 

2. 클래스 메서드

• 클래스가 사용할 메서드
• @classmethod 데코레이터를 사용하여 정의한다.
• 호출 시, 첫번째 인자로 클래스(cls)가 전달된다.
• 클래스를 의미하는 cls 매개변수를 통해 클래스를 조작한다.

class Person:
    def __init__(self, name):
        self.name = name

    @classmethod
    def hello(cls):
        print("안녕", cls.age)

 

 

3. 스태틱 메서드

• 인스턴스 변수, 클래스 변수를 전혀 다루지 않는 메서드 > 즉, 객체 상태나 클래스 상태를 수정할 수 없다.
• @staticmethod 데코레이터를 사용하여 정의한다.
• 일반 함수처럼 동작하지만, 클래스의 이름공간에 귀속된다.
• 언제 사용할까? 주로 해당 클래스로 한정하는 용도로, 속성을 다루지 않고 단지 기능만 하는 메서드를 정의할 때 사용한다.

 

• self

- 인스턴스 자기 자신

- 파이썬에서 인스턴스 메서드 호출 시, 첫번째 인자로 인스턴스 자신이 전달되게 설계된다.

 

• 매직 매서드

- 특정 상황에 자동으로 불리는 메서드

- double underscore(__)가 있는 메서드는 특수한 동작을 위해 만들어진 메서드로, 스페셜 메서드 혹은 매직 메서드라고 불린다.

 

[예시]

__init__(self) : 객체가 생성될 때 호출되는 초기화 메서드
__str__ (self) : 객체를 문자열로 변환할 때 호출되는 메서드. print() 함수와 같은 문자열 변환이 필요한 경우 사용

__eq__(self, other) : 두 객체가 동등한지 판별

 

• 데코레이터

- 파이썬 핵심 기능 중 하나로, 함수를 어떤 함수로 꾸며서 새로운 기능을 부여

- @데코레이터(함수명) 형태로 함수 위에 작성

- 순서대로 적용되기 때문에 작성 순서가 중요

 

데코레이터 예시

def emoji_decorator(func):
    def wrapper(*args, **kwargs):
        func(*args, **kwargs)
        print("^~^")

    return wrapper

@emoji_decorator
def greet(name):
    print(f"안녕, {name}!")

# 데코레이터가 적용된 함수 호출
greet("saeye")

 

실행 

안녕, saeye!
^~^

 

 

상속

 

• 파이썬의 모든 클래스는 object로부터 상속된다.
• 자식 클래스는 부모 클래스의 모든 속성과 메서드를 상속 받는다. > 코드의 재사용성이 높아진다
• super()를 통해 부모 클래스의 요소를 호출할 수 있다.
• 메서드 오버라이딩을 통해 자식 클래스에서 재정의가 가능하다.
• 상속관계에서의 이름 공간은 인스턴스 → 자식 클래스 → 부모클래스 순으로 탐색한다.

---

에러와 예외

 

문법 에러(Syntax Error)

• Syntax Error가 발생하면 파이썬 프로그램은 실행되지 않는다. (정말 많이 봤다...)
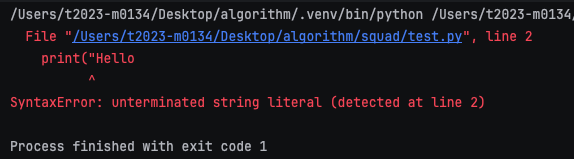
• 파일 이름, 줄 번호, ^ 문자를 통해 파이썬이 코드를 읽어 나갈 때 문제가 발생한 위치를 표현한다.
• 줄에서 에러가 감지된 가장 앞의 위치를 가리키는 캐럿기호 ^ 를 표시한다

 

이런 코드를 작성해서 실행시켜 보면

def greet(name):
    print("Hello

 

이렇게 SyntaxError와 에러가 감지된 줄의 가장 앞의 위치를 가리키고 있는 캐럿기호 ^ 을 확인할 수 있다.

 

 

예외(Exception)

• 실행 도중 예상치 못한 상황을 맞이하면, 프로그램 실행 멈춘다. (문장이나 표현식이 문법적으로 올바르더라도 발생하는 에러)
• 보통 실행 중 감지되는 에러들을 예외(Exception)라고 부른다.
• 예외는 여러 타입이 나타나고 타입이 메시지의 일부로 출려된다. (NameError, TypeError 등이 발생한 예외 타입의 이름)
• 모든 내장 예외는 Exception Class를 상속받아 이뤄진다.
• 사용자 정의 예외를 만들어 관리할 수 있다.

 

 try 문 / except 절을 이용하여 예외처리를 할 수 있다.

 

try문

• 오류가 발생할 가능성이 있는 코드를 실행
• 예외가 발생하지 않으면 except 없이 실행 종료

except 문

• 예외가 발생하면 except 절이 실행
• 예외 상황을 처리하는 코드를 받아서 적절한 조치를 취한다.

* try문은 반듯시 한 개 이상의 except문이 필요하다!

 

예외처리 예시코드

try : 
    num = input('숫자입력 : ')
    print(int(num))
except ValueError:
    print('숫자가 입력되지 않았습니다.')

 

---

 

시간 복잡도 • 공간 복잡도

 

 

기술이 발전한 지금, 우리가 생각해야할 건 시간 복잡도

그럼 우리는 뭘 중요하게 생각하면서 알고리즘을 구현해야 할까?

 

만약 입력의 크기가 n이라면, 알고리즘의 성능은 f(n)

결국 알고리즘의 성능은 주어진 문제의 입력 크기에 따라 달라진다.

---

 

빅오 표기법 (Big-O Notation)

 

말그대로 큰 동그라미 표기법이다. (계산하는게 아닌, 큰 O를 앞에 붙여준 표기법)

입력값이 커질 때 알고리즘의 시간 복잡도(실행시간) 혹은 공간 복잡도(공간 요구사항)이 어떻게 증가하는지 측정하는데 사용된다.

 

빅오로 표현하는 복잡도:
입력값이(n)이 무한대로 커질 때, 함수의 최고 차항만을 표기하고, 계수는 무시한다. (어차피 n 무한대로 보낼거니까)

 

 

예를 들어, f(n) = 9n² + 10n + 3 이 함수의 시간 복잡도는를 구해보자.

 

1. 최고차항만 고려할거니까 == 9n² 

2. 계수는 무시 == n²  

 

빅오로 표현한 시간 복잡도는 O(n²)

 

자, 우리는 이제  f(n) = n2가 뭔지 알아야 한다.

 

응?

---

 

 

다음은 빅오 표기법을 효율성이 좋은 순서대로 나열한 것이다.

 

 

• O(1)  상수 시간 복잡도

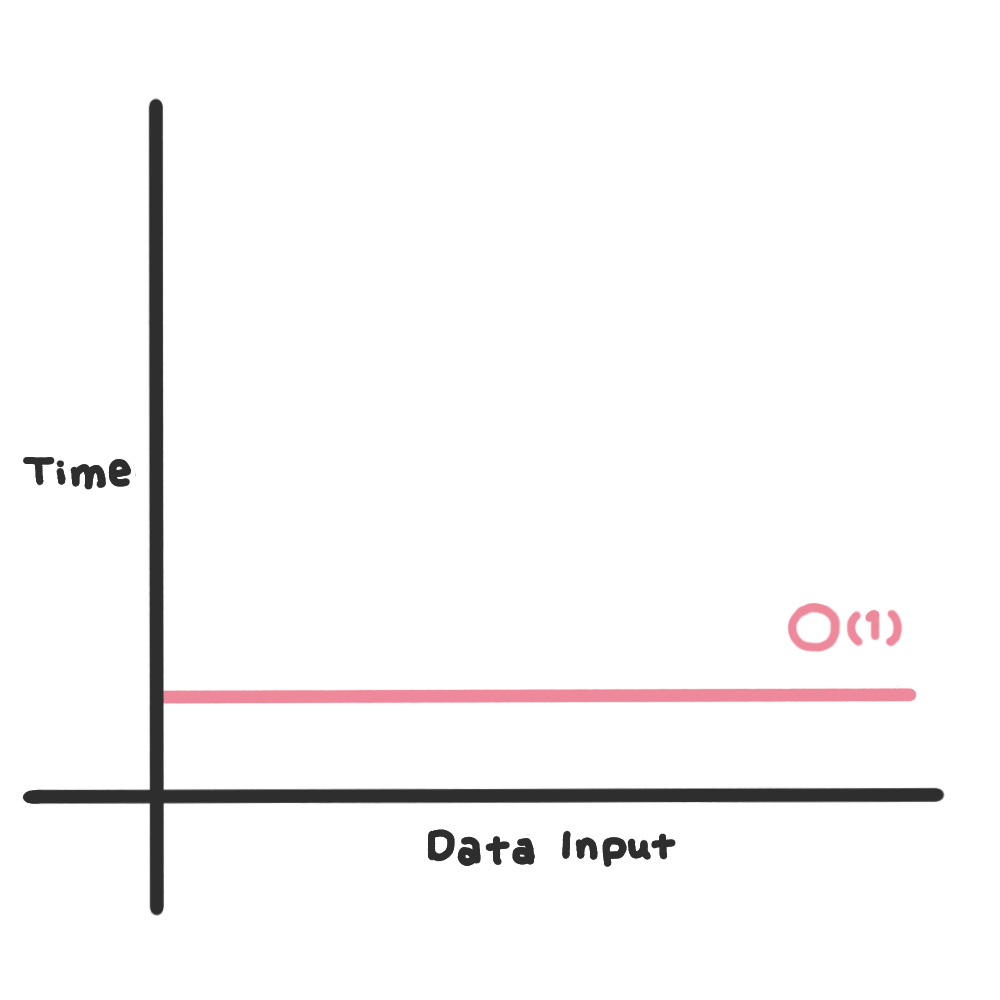
입력값이 아무리 커도 실행시간이 일정한 최고의 알고리즘이다.

O(1)을 따르는 대표적인 알고리즘으로는 해시테이블의 조회와 삽입연산이 있다.

 

 

• O(lon n) 로그 시간 복잡도

로그(log)는 매우 큰 값에도 영향을 많이 받지 않는 특징을 가지고 있다. 즉, f(logn)이 무한대로 가도 크게 영향을 많이 받지 않는다는 것!

이 성질 때문에 우리가 굉장히 큰 값을 다루는 학문에서 대부분 로그를 취해 사용한다.(천문, 지진 관측 등등)

 

 

• O(n) 선형 시간 복잡도

입력값만큼 비례해서 실행 시간에 영향을 받음, 알고리즘을 수행하는 데 걸리는 시간은 입력값에 비례

정렬되지 않은 리스트에서 최대값 또는 최소값을 찾는 경우 등 (모든 값을 뒤적뒤적)

 

 

• O(n lon n) 로그-선형 시간 복잡도

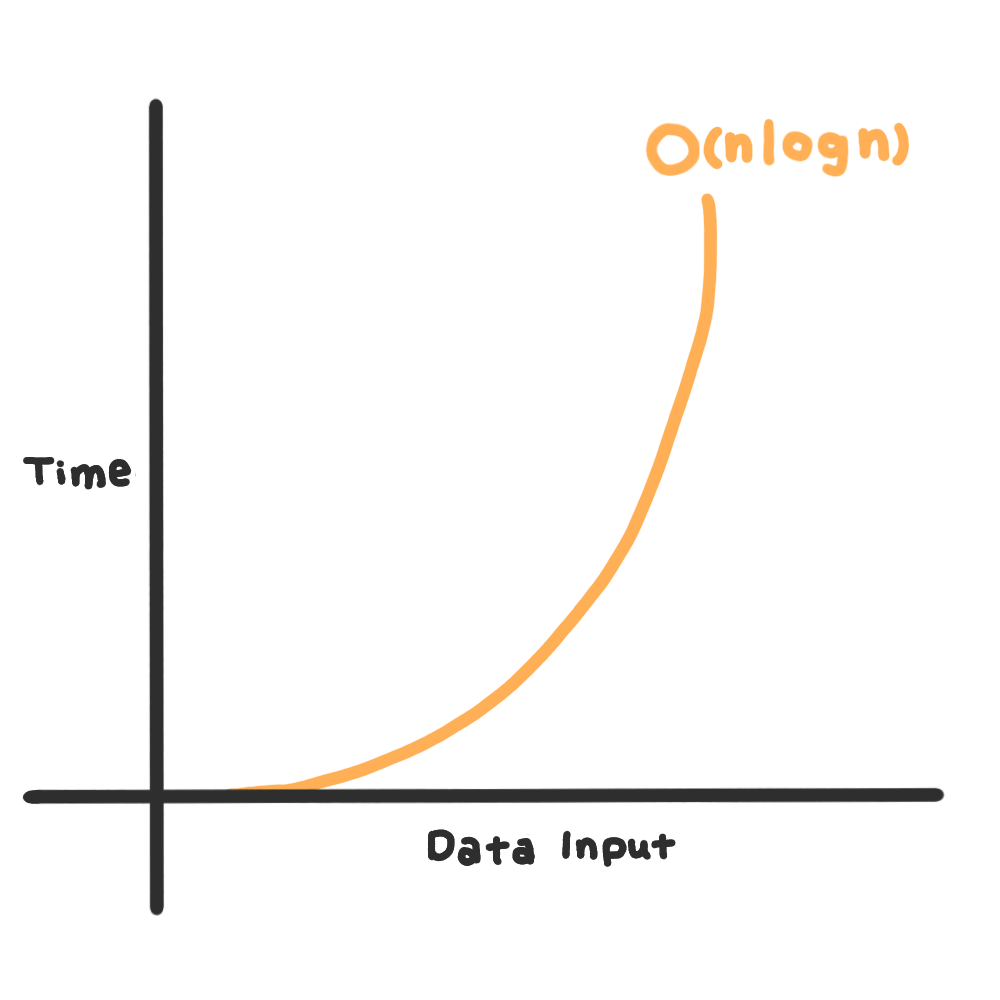
병합 정렬을 비롯한 우리가 일반적으로 알고있는 대부분의 효율 좋은 정렬 알고리즘이 이에 해당

비교 기반 정렬 알고리즘은 아무리 좋은 알고리즘도 얘보다 빠를 수 없음!

물론 입력값이 최선인 경우 O(n)도 될 수 있다. 대표적으로 팀소트(Timsort) 같은 게 있다.

 

 

• O(n²) 이차 시간 복잡도

버블 정렬 같은 비효율적인 정렬 알고리즘이 이에 해당. 반복문이 다른 반복문 안에 포함된 구조인 nested loop에 해당

데이터의 양이 증가함에 따라 실행 시간이 급격히 증가

 

• O(2ⁿ) 지수 시간 복잡도

피보나치의 수를 재귀로 계산하는 알고리즘이 이에 해당

O(n²) 이랑 비교불허, 이놈은 상상을 초월함..ㅋㅋ 입력 크기가 조금만 증가해도 실행 시간이 급격히 증가

 

• O(n!) 팩토리얼 시간 복잡도

외판원 문제(Travelling Salseman Problem) 등에 해당

이걸로 풀면 답은 나와도 써먹을 수 없음.. 입력 크기가 조금만 커져도 계산이 거의 불가능할 정도로 시간이 급격히 증가

(그래도 답이 나오는 알고리즘이라도 짜면 50점, 효율 생각하다가 알고리즘 아예 못 짜면 -1)

 

---

 

그렇다면 이 코드의 시간복잡도는?

def my_func(arr, targer):
    left, right = 0, len(arr)-1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == targer:
            return mid
        elif arr[mid] < targer:
            left = mid + 1
        else:
            right = mid - 1
    return -1

arr = [1, 2, 3, 4, 5]
print(my_func(arr, 4))

 

연산 횟수(배열을 쪼개는 횟수)가 배열의 크기 n까지 가면서 f(n)이 어떻게 변하는지 봐야 한다는데...

음..

내일.. 아니 오늘 다시 해봐야겠다.. 

 

 

 

그나저나... 키보드 ㅋ이 고장났나보다... ㅋ을 칠 때마다 놋북까지 손을 가져가서 ㅋ을 쳐야한다.... 지금 그러고 있다..

ㅣ보드의 ㅣ을 치려고 하면 이렇게 된다. ㅣ을 칠 수 없으니 너무 불편하다. 특히 뒤로 가려고 ㅓ맨드 를 누르려고 할 때 안 되는게 제일 답답하다. 휴..